A continuum method for determining membrane protein insertion energies and the problem of charged residues

Abstract

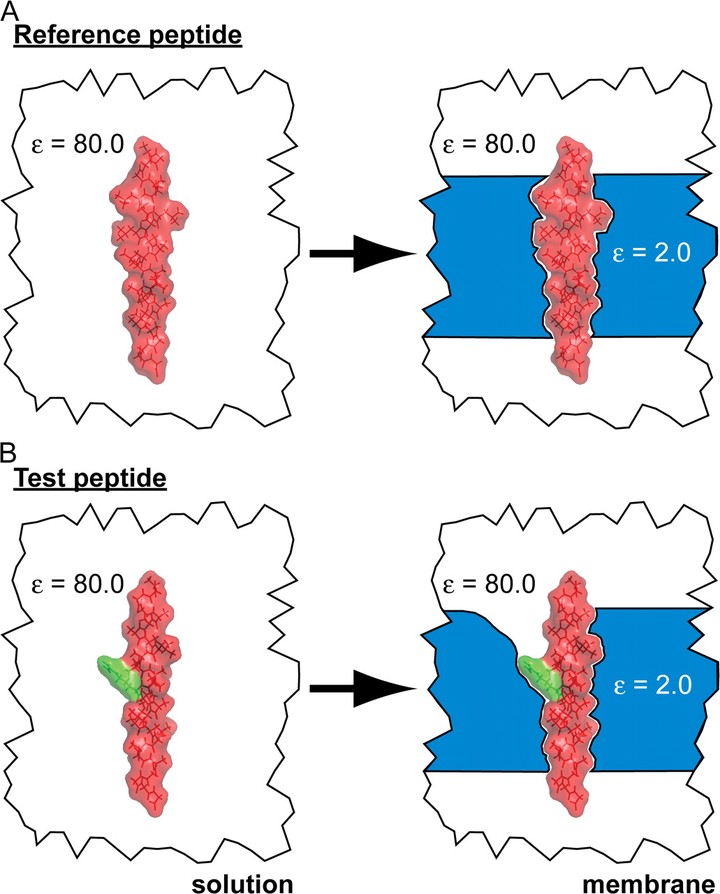
Continuum electrostatic approaches have been extremely successful at describing the charged nature of soluble proteins and how they interact with binding partners. However, it is unclear whether continuum methods can be used to quantitatively understand the energetics of membrane protein insertion and stability. Recent translation experiments suggest that the energy required to insert charged peptides into membranes is much smaller than predicted by present continuum theories. Atomistic simulations have pointed to bilayer inhomogeneity and membrane deformation around buried charged groups as two critical features that are neglected in simpler models. Here, we develop a fully continuum method that circumvents both of these shortcomings by using elasticity theory to determine the shape of the deformed membrane and then subsequently uses this shape to carry out continuum electrostatics calculations. Our method does an excellent job of quantitatively matching results from detailed molecular dynamics simulations at a tiny fraction of the computational cost. We expect that this method will be ideal for studying large membrane protein complexes.